Transformation of Vectors Under Rotation Transformation
A vector is a mathematical object that transforms in a particular way under rotations due to directional character in vector quantity. Let the position vector in cartesian coordinates is given by
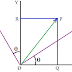
Let the axis of rotation is the z-axis so that the z co-ordinate does not change.
If the x,y coordinates is rotated by q along z-axis.
Since the z-axis does not rotate, so, the z coordinate does not change and we have Z = Z¢
The transformation of vectors under rotation may be described using a rotation matrix. The rotation matrix is applied to the original vector to produce the rotated vector. A rotation around the z-axis would be represented by
This matrix provides a systematic way to express the transformation of vectors under rotation.
Short Questions and their Answers
Q.1. Explain “Transformation of Vectors under Rotation Transformation” .
Ans.
Q.2. If a vector of magnitude A is rotated through certain degree, then what is the change in that
vector?
Ans.
Q.3.Write transformation equation of a vector rotated through q angle.
Ans. Transformation equations of a vector rotated through q angle is given by
Q.4.
Ans.
No comments:
Post a Comment