Transformation of Scalars Under Rotation Transformation

 Transformation of scalars under rotation transformation

A scalar is a mathematical object having magnitude, but no direction which are invariant under
rotation transformation.
The dot product of two vectors is a scalar, and therefore invariant under rotations of the
coordinate system.

 

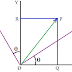
If x, x' are positions in two coordinate system S and S', as the value of the position vector does not change when the coordinate system is rotated, then the relation between positions x and x' in two coordinate system S and S' under rotational transformation is given by

x = x'

 If m, m' are the mass of an object or a particle in co-ordinate system S(x,y,z) and S'(x',y',z'), then under rotation transformation,

m=m'

A scalar quantity is invariant under all possible rotational transformations. The individual
components of a vector are not scalars because they change under transformation.
In classical mechanics, a scalar field is characterized by the fact that its value at a particular
point must be invariant under rotations.
Transformations of scalars are “invariant” under rotation transformation of the coordinate
system.